Wprowadzenie

W stosowanych obecnie systemach transmisyjnych, zasadniczym ograniczeniem przepływności linii jest dyspersja w światłowodzie. Rozróżniamy dwa rodzaje dyspersji, a mianowicie normalną, gdy fale o większej częstotliwości poruszają się wolniej, niż fale o częstotliwości mniejszej oraz anomalną jeżeli jest odwrotnie. Typowe jednomodowe światłowody telekomunikacyjne wykazują zero dyspersji dla długości fali równej 1,31 μm. Poniżej tej długości fali występuje dyspersja normalna, zaś powyżej anomalna. Krótkie impulsy mają szerokie widmo, stąd dyspersja powoduje różnicę prędkości rozchodzenia się składowych częstotliwościowych impulsu (jego widma) i jego deformację. Poszerzenie impulsu rośnie z odległością transmisji i powoduje nierozróżnialność kolejnych impulsów.

Zainteresowano się zatem zjawiskami nieliniowymi mogącymi kompensować dyspersję.

Teoria rozchodzenia się solitonów

Szkło kwarcowe wykazuje słabą nieliniowość optyczną tzn. jego współczynnik załamania n wskutek efektu Kerra zależy od natężenia światła i, co można zapisać następująco:n = n⁰ + n² * i, gdzie: n⁰- wartość współczynnika przy natężeniu światła bliskim zeru, n² - nieliniowy współczynnik załamania o wartości 3,18*10ˉ²⁰ m²/w. Takie właściwości nieliniowe światłowodu mogą skompensować poszerzenie impulsu powodowane dyspersja. Daje to możliwość przesyłania impulsów zachowujący swój kształt czasowy tzw. solitonów. Nieliniowość światłowodu powoduje to, że w miejscu dużego natężenia impulsu świetlnego n wzrasta, zatem prędkość fali maleje. W rezultacie środkowa część impulsu porusza się wolniej niż jego czoło oraz tył, zaś częstotliwość ulega zróżnicowaniu - przednia część impulsu doznaje zmniejszenia częstotliwości, a tylny zwiększenia częstotliwości [1].

Do kompensacji nieliniowego poszerzenia czoła impulsu, dyspersja powinna zwalniać w większym stopniu czoło impulsu, o zmniejszonej częstotliwości, niż jego resztę, czyli powinna to być dyspersja anomalna. W przypadku tej dyspersji zjawisko nieliniowości i dyspersja światłowodu mogą się wzajemnie kompensować. Możliwy jest taki dobór kształtu impulsu, jego amplitudy i czasu trwania, że oba powyższe efekty dokładnie się zniosą. Takie impulsy to solitony, a propagacja solitonu podstawowego w światłowodzie na rysunku obok (Rys. 1).

Jeżeli impuls o kształcie secansa hiperbolicznego, którego szerokość T₀ i moc szczytowa P₀ spełniają zależność: N = √ (γ*P₀*T₀²) / lβ”I = 1, zostanie wprowadzony do idealnego bezstratnego światłowodu, będzie się rozchodził bez zmiany kształtu na dowolnie duże odległości. We wzorze: γ - parametr nieliniowości odpowiedzialny za modulację własną fazy, β” - parametr określający dyspersję prędkości grupowej. Moc szczytowa solitonu podstawowego wymagana do prowadzenia go przez światłowód może być określona w łatwy sposób z zależności na N, przy czym jej wartość jest ściśle związana z właściwościami danego światłowodu tj. nieliniowością i dyspersją.

Słowo ,,soliton” oznacza samotną, odosobnioną falę. Solitony mają swoją własną prędkość, która zależy od ich energii. Są one wyraźnie zlokalizowane w czasie i w przestrzeni, nawet w wyniku spotkania i kolizji z innymi solitonami zachowują swoje istnienie i zazwyczaj ponownie się separują. Jedyne co może okazać się destrukcyjne dla ich istnienia, to straty mocy powodowane tłumiennością światłowodu, a w konsekwencji zanik efektów nieliniowych.

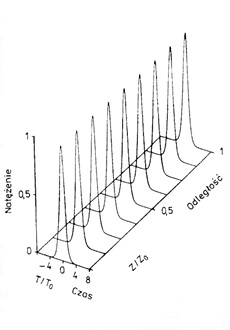
Rysunek 1. Propagacja solitonu podstawowego w światłowodzie [1].

W światłowodach kwarcowych występują cztery rodzaje nieliniowych efektów optycznych, a mianowicie wzmocnienie Ramana, wzmocnienie Brillouina, mieszanie czterofalowe oraz efekt Kerra. Transmisja solitonowa jak już wcześniej wspomniano oparta jest na efekcie Kerra.

Analogia pomiędzy solitonem, a modem

Mody zachowują w czasie propagacji swój kształt, czyli rozkład przestrzenny pola w przekroju poprzecznym w falowodzie w wyniku idealnej kompensacji dwóch przeciwstawnych efektów: poprzecznego poszerzenia dyfrakcyjnego wynikającego z ograniczoności poprzecznej wiązki oraz ogniskowania wiązki przez falowód. Zatem dyfrakcja + ogniskowanie = 0. Podobnie, soliton podstawowy zachowuje swój kształt czasowy w wyniku idealnej kompensacji dwóch przeciwstawnych efektów: dyspersyjnego poszerzenia w czasie wynikającego z ograniczoności czasowej impulsu oraz zniekształcenia nieliniowego. Więc dyspersja + nieliniowość = 0 (Rys. 2).

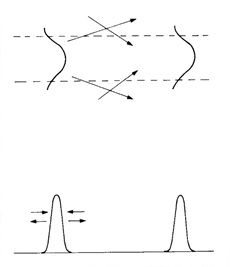
Rysunek 2. Analogia między propagacją modu światłowodowego i solitonu podstawowego. Dla modu (u góry) efekt dyfrakcji jest dokładnie kompensowany przez efekt ogniskowania w rdzeniu. Dla solitonu podstawowego efekt ten kompensuje nieliniowość światłowodu [1].

Solitony wyższych rzędów i solitony ciemne

Wyróżnia się soliton podstawowy, zachowujący kształt przez cały czas propagacji oraz solitony wyższych rzędów okresowo odtwarzające swój kształt. W telekomunikacji jak dotąd znalazły zastosowanie solitony podstawowe. Solitony wyższych rzędów stosuje się w labolatoriach do generacji ultrakrótkich, femtosekundowych impulsów. Taki soliton rozpoczyna propagację jako pojedyńczy impuls, w trakcie propagacji zmienia swój kształt, a następnie odtwarza początkowy (Rys. 3).

Solitony ciemne powstają w wyniku obniżenia natężenia (P₀) fali ciągłej.

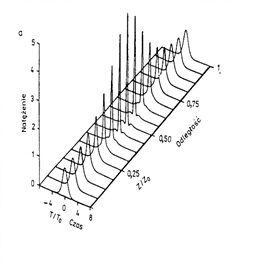
Rysunek 3. Propagacja w światłowodzie solitonu drugiego rzędu N = 2 [1].

Straty i oddziaływania między solitonami

Solitony są atrakcyjne dla komunikacji optycznej ze względu na ich zdolność zachowania kształtu nawet w dyspersyjnym światłowodzie. Ta ich własność jest prawdziwa wtedy, gdy straty w światłowodzie są do pominięcia. Zmniejszenie energii spowodowane stratami w światłowodzie prowadzi do rozszerzenia solitonu. Jak się okazuje nieliniowość światłowodu powoduje również oddziaływanie między sąsiednimi solitonami. Odstęp czasu między sąsiednimi bitami lub impulsami wyznacza szybkość transmisji systemu telekomunikacyjnego, zatem kluczową sprawą jest określenie bezpiecznej odległości między nimi.

Jeżeli solitony mają jednakowe fazy, wówczas przyciągają się i w rezultacie zlewają się ze sobą (Rys. 4).

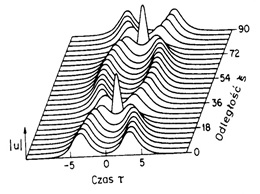
Rysunek 4. Zlewanie się solitonów o jednakowej fazie [2].

Natomiast jeśli fazy kolejnych solitonów są przeciwne, odpychają się one i tworzą równoległe ,,garby”. Odpowiednia odległość niemal pięciokrotnie większa od ich szerokości, eliminuje oddziaływanie między nimi (Rys. 5).

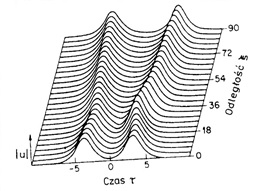
Rysunek 5. Odpychanie się solitonów o przeciwnych fazach [2].

System transmisji solitonowej

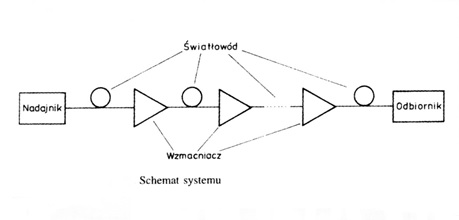
Rysunek 6. Schemat blokowy systemu do transmisji solitonowej [3]. Układ składa się z nadajnika, światłowodu, systemu wzmacniaczy oraz odbiornika.

Podsumowanie

Pomimo tego, że teoria solitonu oraz jego własności propagacyjne były znane już w 1895 roku, to pierwszą emisję impulsu solitonowego zademonstrowano dopiero w 1980 roku Mollenauer, Stolen i Gordon, otwierając tym samym nową dziedzinę optoelektroniki - solitronikę, działającą w obszarze impulsów pikosekundowych i femtosekundowych. Do 1990 roku wykonano szereg eksperymentalnych transmisji, uzyskując pojemność transmisyjną o przepływności 10 Gb/s na odległość 36 000 km, a więc prawie wokół całej kuli ziemskiej. Niewątpliwie ta nowa technologia światłowodowa doprowadziła do znacznego postępu w telekomunikacji i nadal będzie kluczową dziedziną w przesyłaniu sygnałów na duże odległości.

Autor: Karolina Wójciuk

Literatura

1. Drazin, P.G., Johnson, R.S., 1989. Solitons: an introduction. Cambridge University Press.
2. skaczmarek.zut.edu.pl/Wyklad21.ppt‎
3. www.skaczmarek.ps.pl/Wyklad19.pdf